Definisi Limit dan Notasinya

Perhatikan suatu fungsi f(x) dan misalkan suatu variabel bebas x mengambil nilai dekat sekali dengan bilangan konstan a, maka f(x) akan mempunyai suatu himpunan nilai sesuai dengan nilai-nilai yang diambil oleh variabel x tadi.

Misalnya ktika x dekat dengan a, nilai fungsi f(x) yang berhubungan dengan nilai tersebut makin mendekati A, suatu bilanan konstan. Selanjutnya kita misalkan bahwa nilai-nilai f(x) dapat dibuat menjadi begitu dekat dengan A sehingga jarak atau selisihnya kecil sekali dengan jalan mengambil nilai-nilai x yang juga sangat dekat dengan a akan tetapi tidak sama dengan a tersebut dan ini benar untuk semua nilai x. Kemudian f(x) dikatakan mendekati limi A ketika x mendekati a. Lebih tepatnya, definisi mengenai liit suatu variabel dan limit suatu fungsi adalah sebagai berikut :

Suatu variabel x dikatakan mendekati konstan a sebagai limit ketika x berubah sedemikan rupa sehingga perbedaan mutlax I x – a I menjadi dan tetap lebih kecil dari setiap bilangan positif yang telah ditentukan sebelumnya betapapun kecilnya bilangan ini dipilih. Hal ini ditunjukan dengan notasi :

Limit x = atau x → a

Contoh :

Kalau x mengambil urutan nilai-nilai :

½, 3/3, 7/8, .... , (2ⁿ – 1 )2ⁿ

Maka dikatakan x → 1, artinya satu merupakan limit dari x. Akan tetapi kalu x mengambil urutan nilai-nilai :

½, -3/4, 7/8, -15/16, .... , (-1)^n-1 ((2ⁿ – 1)/2ⁿ),...

Maka x tak akan mencapai suatu limit kalau fungsi f(x) mendekati suatu bilangan konstan A, ketika x mendekati , akan tetapi tidak pernah mengambil nilai a. A dikatakan merupakan limit (batas) f(x) ketika x mendekati A.

lim _{x → a} f(x) = A atau f(x) → a ketika x → a

Contoh :

Kalau f(x) = 2x + 5, lim _{x → a} f(x) = 5, sebab kalau x semakin kecil sehingga mendekati 0, nilai f(x) mendekati 5 seperti ilustrasi berikut ini :

f(1) = 7

f(1/2) = 6

f(1/4) = 5 ½

f(1/100) = 5 1/50

f(1/1000) = 5 1/500

dan sebagai nya...

atau :

f(-1) = 3

f(-1/2) = 4

f(-1/4) = 4 ½

f(-1/100) = 5 49/50

f(-1/1000) = 4 499/500

dan sebagainya ....

Dua pernyataan berikut mengenai definisi limit suatu fungsi sama dengan definisi di atas yaitu :

Suatu fungsi f(x) dikatakan mendekati suatu limit A ketika x mendekati a, apabila selisih atau perbedaan mutlak antara f(x) dan A lebih kecil dari suatu bilangan positif yang sangat kecil untuk setiap nilai x yang sangat dekat dengan a dan untuk mana x ≠ a (ingat x → a berarti x ≠ a)

Suatu fungsi f(x) mendekati suatu limit A ketika x mendekati a, jika dan hanya jika, untuk setiap ϵ > 0 terdapat suatu nilai δ sedemikian rupa sehingga ketika 0 < I x – a I < δ maka :

І f(x) – A І < ϵ, di mana :

δ = delta

ϵ = epsilon

Dari uraian di atas mengenai pengertian limit, dapat di artikan bahwa kedua x dan f(x) mendekati suatu bilangan konstan yang terbatas (finite constant), masing-masing a dan A sebagai limit atau batas. Bisa juga terjadi salah satu atau keduanya menjadi sangat besar atau sangat kecil secara seimbang.

Perhatikan definis berikut :

Apabila perbedaan antara suatu fungsi f(x) dan suatu konstan A menjadi semakin kecil secara mutlah (ablsolut); untuk semua nilai positif dari x yang cukup besar, maka kemudian f(x) dikatakan mendekati A sebagai suatu limit ketika x menjadi tak terhingga secara positif, yaitu meningkat terus tanpa batas. Hal ini bisa ditunjukan dengan notasi berikut :

Lim _{x → ∞} f(x) = A atau f(x) → A ketika x → ∞

Contoh :

Jika f(x) = 1 – (1/x), kemudian lim _{x → ∞}f(x) = 1, sebab :

f(1) = 0

f(5) = 4/5

f(20) = 19/20

f(100) = 99/100

f(1000) = 999/1000

f(10.000) = 9999/9.000

dan seterusnya...

Demikian juga halnya, limit f(x) mungkin didefinisikan ketika x menuju kenilai tak terbatas negatif, yaitu menurun tanpa batas. Hal ini ditunjukan dengan notasi sebagai berikut :

Lim _{x → -∞} f(x) = A’ atau f(x) → A’ ketika _{x → -∞}

Contoh :

Jika f(x) = 1 – (1/x), kemudian Lim _{x → -∞} f(x) = 1

Jika suatu fungsi f(x) lebih besar dari suatu bilangan positif yang besar sembarang untuk semua nilai x yang sangat dekat dengan suatu bilangan konstan a dan untuk mana x ≠ a, kemudian f(x) dikatakan menjad positif tak terbatas yaitu meningkat tanpa batas ketika x mendekati a. Hal ini ditunjukan dengan notasi sebagai berikut :

lim _{x → a} f(x) = ∞ atau f(x) → ∞ ketika x → a

Demikian juga halnya, limit f(x) mungkin didefinisikan ketika x menuju ke nilai tak terbatas negatif, yaitu menurun tanpa batas. Hal ini ditunjukan dengan notasi sebagai berikut :

lim _{x → a} f(x) = -∞ atau f(x) → -∞ ketika x → a

Contoh :

Jika f(x) = 1/(x – 1)2, kemudian lim x → 2 f(x) ∞

Jika suatu fungsi f(x) lebih besar dari pada suatu bilangan positif yang sangat besar sembarang (arbitraly large) untuk semua nilai x yang cukup besar, maka kemudian f(x) dikatakan menjadi positif tak terbatas, artinya meningkat tanpa batas ketika x menjadi positif tak terbatas yaitu meningkat tanpa batas.

Hal ini dapat ditunjukan dengan notasi sebagai berikut :

lim _{x → ∞} f(x) = ∞ atau f(x) → ∞ ketika x → ∞

kasus-kasus dengan notasi sebagai berikut, didefiniskan sama :

lim _{x → ∞} f(x) = -∞ atau f(x) → -∞ ketika x → ∞

lim _{x → -∞} f(x) = ∞ atau f(x) → ∞ ketika x → -∞

lim _{x → -∞} f(x) = -∞ atau f(x) → -∞ ketika x → -∞

Contoh :

Jika f(x) = x4 – 4, kemudian lim _{x → ∞}f(x) = ∞ dan lim _{x → -∞} f(x) = -∞

Di dalam beberapa kasus, suatu fungsi mungkin mendekati salah satu dan dua limit yang berbeda, tergantung pada kenyataan apakah variabel mendekati limitnya melalui nilai yang lebih besar atau lebih kecil dari pada limit, dalam hal semacam itu, limit tidak terdefinisi (tak ada) akan tetapi limit sebelah kiri atau kanan ada.

Limit sebelah kanan (right hand limit)

Suatu fungsi merupakan nilai yang didekati fungsi, ketika variabel mendekati limitnya melalui nilai yang menurun, dari pada sebelah kanan; tipe kelakuan/tingkah laku dari limit ini ditunjukan dengan notasi sebagai berikut :

lim _{x → a⁺} f(x) = A⁺ atau f(x) → A⁺ ketika x → A⁺

Limit sebelah kiri (left hand limit)

Suatu fungsi mendekati nilai yang didekati fungsi, ketika variabel mendekati limitnya melalui nilai meningkat dari sebelah kiri; ini ditunjukan oleh notasi berikut ini :

lim _{x → a^- f}(x) = A^- atau f(x) → A^- ketika x → A^-

Jadi limit suatu fungsi ada jika dan hanya jika limit sebelah kiri dan kanannya ada dan sama nilainya; dalam hal ini maka :

lim _{x → a⁺} f(x) = lim _{x → a^-}f(x)= lim _{x → a}f(x)

Contoh :

Jika f(t) = [t] = bilangan bulat terbesar dalam t, kemdian

lim _{t → 3⁺} f(t) = 3 dan lim _{t → 3^-1} f(t) = 3-1

Jadi lim _{x → 3} f(x) tak terdefinisi (tidak ada)

Kelihatannya mungkin bahwa limit dari fungsi f(t) ketika t → 3 harus 3. Akan tetapi, ketika t secara sembarang mendekati 3, beberapa nilai [t] adalah 2, jika t < 3, jika t > 3. Jadi nilai-nilai t tidak mendekati salah satu nilia A ketika t secara sembarang mendekati 3 dan lim t → 3 [t] tidak ada, walaupun limit sebelah kiri dan kanan sama, akan tetapi tak sama besarnya. Hal ini ditunjukan pada gambar IV.I. dengan garis horizontal yang tidak terputus-putus antara bilangan bulat t yang berurutan.

Fungsi f(t) mendekati 2 ketika x mendekati 3 dari sebelah kiri dan mendekati 3 ketika x mendekati 3 dari sebelah kanan. Yang jelas tak ada yang unik tentang angka 3; kenyataanya f(t) tak mempunyai limit (walaupun mempunyai limit sebelah kiri dan kanan) ketika t mendekati setiap bilangan bulat; akan tetapi f(t) mempunyai limit ketika t mendekati nilai yang tidak bulat.

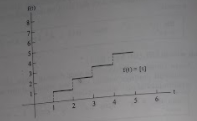Gambar IV.I. Kurve fungsi f(t) = t

Contoh :

Jika f(t) = 1/t, kemudian

lim _{t →0⁺} f(t) = ∞ dan lim _{t →0^-} f(t) = -∞(Lihat gambar IV.2)

Gambar IV.2 Kurve fungsi f(t) = 1/t

Jika lim f(t) tak terdefinisikan; ketika t mendekati 0 dari atas, f(t) menjadi tak terhingga secara positif, ketika t mendekati 0 dari bawah f(t) menjadi tak terhingga secara negatif.

Bisa juga terjadi perubahan limit sebelah kiri dan kanan tak ada, sebagai contoh, fungsi sinus dan cosinus yang sifatnya selalu bergoyang (oscillatory in nature).

Sekian artikel kali ini. Mohon maaf apabila ada salah-salah kata.

Akhir kata wassalamualiakum wr. wb.

Referensi :