Hallo temen-temen???
Pertama-tama gue ucapin trimakasih buat para pengunjung blog gue :). Slamat datang di blog paling bermanfaat sedunia.
Dan gue doaian semoga orang-orang yang ngunjungin blog gue pada masuk surga semua, trs selama hidupnya selalu di beri kemudahan, trs all the best deh buat kalian :D
Udah kaya ulang tahun aja ya ???.... Sorry ya klo penulis suka bercanda :)
Kembali lagi bersama gue muhamad pajar sidik, gue adalah seorang penulis blogger yang ganteng dan baik hati :D cieeee.....
Di hari yang indah ini alhamdulillah gue bisa nulis artikel kembali, yang mudah-mudahan artikel ini bisa bermanfaat buat kalian semua.
Kali ini gue bakalan nulis artikel tentang Tabel Kebenaran Logika Matematika, Tanpa panjang lebar lagi yo check it out !
Ktika sesama manusia saling bersosialisasi maka akan terciptalah suatu komunikasi. Komunkasi antar manusia biasa dilakuakan dengan cara berdialog satu sama lain. Ktika manusia berdialog maka mereka harus saling memahami dialog mereka satu sama lain. Di dalam suatu dialog, pasti ada pesan - pesan atau makna tertentu. Makna tersebut biasanya berupa berita atau pengetahuan baru yang dimana harus dicerna dahulu dengan logika terkait benar atau tidaknya berita atau pengetahuan tersebut. Terkait pernyataan tersebut terciptalah ilmu logika matematika, yang dimana dengan logika matematika, kita dapat mengetahui nilai kebenaran suatu pernyataan. Nilai kebenaran tersebut disajikan dalam tabel untuk memahaminya. Ada beberapa tabel dasar kebenaran dari suatu logika matematika, diantaranya :
1. Tabel Kebenaran Ingkaran Atau Negasi
Ingkaran atau negasi adalah suatu kebalikan atau lawan dari suatu pernyataan. Misalkan ada sebuah pernyataan p bernilai benar, maka negasi dari pernyataan p tersebut adalah bernilai salah. Untuk pernyataan negasi diberi simbol "~". Untuk tebel kebenarannya bisa dilihat gambar di bawa ini :
 |
| Tabel Kebenaran Ingkaran atau Negasi |
2. Tabel Kebenaran Konjungsi
Konjungsi merupakan gabungan dari dua pernyataan tunggal dengan menggunakan kata hubung "dan". Simbol dari konjungsi adalah "^". Untuk Lebih jelasnya perhatikan gambar di bawah ini :
 |
| Tabel Kebenaran Konjungsi |
Nah tabel kebenaran tersebut pun ada hukumnya, dimana jika nilai kedua pernyataan bernilai benar, maka nilai kebenaran konjungsi kedua pernyataan tersebut pun benar, dan apabila ada salah satu pernyataan yang bernilai salah, maka nilai konjungsi kedua pernyataan tersebut pun bernilai salah.
3. Tabel Kebenaran Disjungsi
Disjungsi merupakan gabungan dari dua pernyataa tunggal yang menggunakan kata hubung "atau". Simbol dari disjungsi adalah "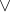 ". Untuk tabel kebenarannya perhatikan gambar di bawah ini :
". Untuk tabel kebenarannya perhatikan gambar di bawah ini :
 |
| Tabel Kebenaran Disjungsi |
Dalam menentukan nilai kebenaran disjungsi pun memiliki aturan yaitu, jika salah satu dari dua pernyataan bernilai benar, maka nilai kebenaran disjungsi dari kedua pernyataan tersebut adalah benar, dan apabila kedua pernyataan tersebut bernilai salah, maka nilai kebenaran disjungsinyapun bernilai salah.
4. Tabel Kebenaran Implikasi
Impilakasi ada gabungan dari dua pernyataan tunggal dengan kata hubung "jika, maka". Simbol dari implikasi adalah "→". Untuk tabel kebenarannya perhatikan gambar di bawah ini :
 |
| Tabel Kebenaran Implikasi |
Untuk atauran menentukan nilai kebenaran dari implikasi adalah, jika nilai pernyataan yang ke-dua dari dua penrnyataan bernilai benar dan jika ke-dua pernyataan bernilai sama baik itu benar ataupun salah, maka nilai kebenaran implikasi adalah benar, dan apabila nilai kedua pernyataan tersebut beda dengan pernyataan ke-duanya bernilai salah, maka nilai kebenaran implikasi dari dua pernyatan tersebut bernilai salah.
5. Tabel Kebenaran Biimplikasi
Biimplikasi adalah gabungan dari dua pernyataan tunggal dengan kata hubung "jika dan hanya jika, maka ". Simbol dari biimplikasi adalah "↔". Untuk nilai kebenarannya perhatikan tebel di bawah ini :
 |
| Tabel Kebenaran Biimplikasi |
6. Tabel Kebenaran Negasi Konjungsi
Untuk tabel kebenaran negasi konjungsi ini dimana berlaku negasi dari p ∧ q equivalen dengan ~p ∨ ~q. Untuk tabel kebenarannya lihat tabel di bawah : |
| Tabel Kebenaran Negasi Konjungsi |
7. Tabel Kebenaran Negasi Disjungsi
Untuk nilai kebenaran disjungsi dimana berlaku negasi dari p ∨ q ekuivale dengan ~p ∧ ~q. Untuk tabel kebenarannya perhatikanlah tabel di bawah :
 |
| Tabel Kebenaran Negasi Disjungsi |
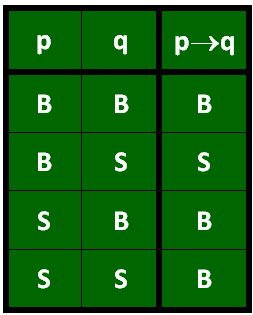
8. Tabel Kebenaran Negasi Implikasi
Nilai kebenaran negasi implikasi yang dimana negasi dari p→q ekuivalen dengan p∧~q , maka tabel kebenarannya adalah :
 |
| Tabel Kebenaran Negasi Implikasi |
9. Tabel Kebenaran Negasi Biimplikasi
Negasi dari p↔q ekuivalen dengan (p ∧ ~q) ∨ (q ∧ ~p), Maka nilai kebenarannya adalah :
 |
| Tabel Kebenaran Negasi Biimplikasi |
Kesimpulan
Jadi untuk menentukan pernyataan bernilai salah atau benar, dalam matematika ada ilmunya yaitu dengan cara menentukan tabel kebenaran.
Keterangan :
Maksud B dan S pada tabel adalah dimana B itu Bernilai benar dan S bernilai salah.
Sekian dulu ya artikel kali ini. Mohon maaf apa bila ada kesalahan
Baca juga artikel tentang :
Akhirkata wassalamualaikum wr. wb.
Jika ingin bertanya secara privat, Silahkan hubungi no 085709994443 dan untuk berkomentar silahkan klick link di bawah ini 👇
