simak ya !
A. Relasi
Jika diketahui himpunan A dan himpunan B maka suatu relasi dari himpunan A ke himpunan B adalah pemasangan anggota himpunan A dengan anggota himpunan B dengan suatu aturan tertentu.
Contoh Relasi :
Relasi A ke B = Relasi Kegemaran
B. Fungsi atau Pemetaan
Pemetaan atau fungsi dari A ke B adalah relasi khusus yang memasangkan setiap anggota A dengan tepat satu anggota B.
Contoh fungsi atau pemetaan :
Dari contoh gambar disamping diperoleh :
A = {a,b,c} disebut daerah asal (domain)
B = {u,v,w,x} disebut daerah kawan (kodomain)
{w,u} pada (ii) disebut daerah hasil (range)
Sekarang kita membedakan mana yang merupakan fungsi dan mana yang bukann merupakan fungsi
Perhatikan gambari dibawah ini :
1. diagram venn X bukan merupakan fungsi karena ada anggotanya yaitu b memiliki lebih dari satu pasangan.
2. diagram venn Y merupakan fungsi karena setiap anggotanya domainnya memiliki tepat satu pasangan .
C. Notasi Fungsi
Fungsi x yang memetakan ke y = ax + b dapat dituliskan dengan notasi f : x ® ax + b atau f(x)=ax+b
Perhatikan gambar di samping !
dari gambar di samping bahwa :
x = {0,1,2,3} adalah domain (daerah asal)
y = {7,10,13,16} adalah kodomain {daerah kawan}
dan daerah y yang terkena panah dari tiap anggota daerah x seperti {7,10.13,16} adalah range (daerah hasil)
notasi fungsi pada gambar di samping adalah :
f : x ® 3x + 7 atau f(x)=3x+7
D. Bentuk Penyajian Relasi dan Fungsi
1. Menggunakan diagram panah
2. Menggunakan himpunan pasangan berurutan
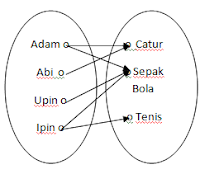
Contoh :
{(Adam, Catur), (Adam, Sepak bola), (Abi, Catur), (Upin, Sepak bola), (Ipin Sepak bola), (Ipin, Tenis)}
3. Menggunakan diagram cartesius.
E. Banyaknya Pemetaan, Banyaknya Himpunan Pasangan Berurutan, dan Korespondensi
a. Banyaknya pemetaan yang mungkin dari dua himpunan. Jika, n(X) = k dan n(Y) = m, maka banyaknya pemetaan dari himpunan x ke y adalah mk
Contoh :
X = {1,2,3}
Y = {x,y}
maka banyaknya pemetaan yang mungkin dari X ke Y adalah : 23 = 8
b. Banyaknya himpunan pasangan berurutan dari dua himpunan (dari himpunan X ke Y), dinotasikan X x Y · X x Y = n(X) · n(Y)
Contoh :
X = {1,2,3}
Y = {a,b}
X x Y · X x Y = n(X) · n(Y)
= 3 · 2
= 6
c. Banyaknya koerespondensi satu-satu dari dua himpunan (dengan syarat n(X) = n(Y)) adalah perkalian berurutan.
Contoh :
X = {1,2,3,4}
Y = {a,b,c,d}
maka banyaknya korespondensi satu-satu himpunan X dan Y adalah :
4x3x2x1 = 24
Nah segini dulu yah materi dari saya
mohon maaf apabilan ada kesalahan
jika ada yang ingin ditanyakan silahkan komentar saja yah
assalamualaikum bye - bye ......
Jika ingin bertanya secara privat, Silahkan hubungi no 085709994443 dan untuk berkomentar silahkan klick link di bawah ini 👇
